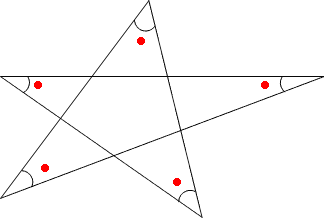
角度の求め方 算数の教え上手 学びの場 Com
平行四辺形のなかの三角形の相似や角度、長さ、等しい面積の求め方 中学の数学の解き方の詳しい解説ノートです。ノートの取り方も参考にしてください。ノートはクリックで拡大します。 現役 三角形の面積は「 底辺 高さ 底 辺 × 高 さ ÷ 2 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形
[ベスト] 円の面積 おもしろ問題 164528-円の面積 面白問題
円の面積 複雑でよく間違える計算なので助かった。 食卓を買い替えるにあたり、丸ちゃぶ台サイズ90φか100φかかなり悩みました。 いっそ間をとって95φもありかなと思ったり。 ちなみに現テーブルは長方形90×60。 夫が現テーブルを手狭に感じている ただ、はじめて円の面積の公式 (半径 × 半径 × 314) を習ったとき、まったく理解できなかったんですよね。いったいなんでそうなるのかと。 そんなとき、ドラえもん算数シリーズの「面積・体積」に載っていた (違うかも。 問題 （正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する） 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の
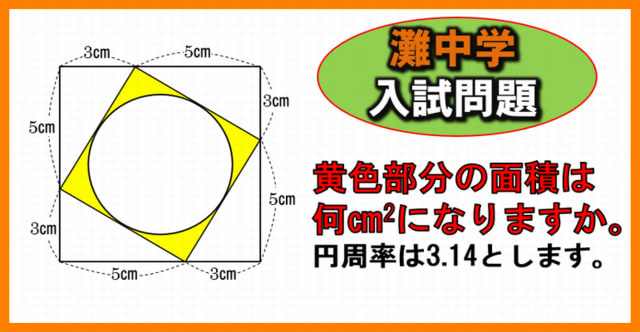
灘中学入試問題 全2問 ありがちな良問 暇つぶしに動画で脳トレ
円の面積 面白問題
√ 5年生 算数 平均 343833
算数 5年生 第12節 × 平均 基本をマスターしよう！ fc町田ゼルビアのホームゲームにおける、 過去5年間の町田gionスタジアムの観客動員数を調べたところ、 右の表のようになりました。(百の位を四捨五入して、がい数で表示)この5年間の平均の観客動員数を求めましょう。SAPIX5年生 年10月14日（水）17時～実施の、歴史初を含んだマンスリーテストの平均点です 平均点 2811点 算数 平均8点 国語 平均856点 理科 平均539点 社会 平均5点 4教科平均は、夏期講習マンスリーより15点ほどUP。 算数と社会が平気点上がり次の文は、平均のきまりです。よく読んで理解しましょう。 うすい字はなぞり書きをしましょう。 いくつかの数量を、同じ大きさ（分量）になるようにならしたものを、 それらの数量の平均といいます。 平均は〔数量の合計〕÷〔個数〕で求められます。 2
5年生算数 速さ 黒板log
5年生 算数 平均
[新しいコレクション] 三角形の角度の求め方 小学生 820649-三角形の角度の求め方 小学生
答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を 三角関数の角度を求めるときは、θの範囲を忘れないこと それぞれの求め方をまとめると 単位円 を書いて、三角関数に適した直線を書き込み交点を求める。 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるか二等辺三角形の２つの底角は等しいです。 よって、 ∠ C の大きさも 50 ∘ です。 よって、 ∠ B ∠ C = 100 ∘ です。 三角形の内角の和は 180 ∘ なので、 ∠ A の大きさは、
角度の求め方 算数の教え上手 学びの場 Com
三角形の角度の求め方 小学生
[最も好ましい] 平行 角度 302732-平行 角度 求め方
平行是一個幾何學術語。 在平面幾何中，永遠不會相交的多條直線，或者多個平面彼此互相平行。 在歐幾里得幾何中，由平行公設，一個平面上的直線外指定一個點，就能指定出一條與它平行的直線。 在非歐幾何中，根據空間曲率的不同，在一條直線外指定一個點可以作多條或零條與它平行的直線。753 两平面的夹角 定义 两张平面的法向量的夹角（通常指 锐角 ）称为 两平面的夹角 。 设平面Π 1 和Π 2 为： 它们的法向量依次为： 、 ， 记平面Π 1 和Π 2 的夹角 ，由规定 应是锐角，因此 的余弦值非负。 （6） 从两向量垂直、平行的充分必要条件立即推得下列结论：平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 1
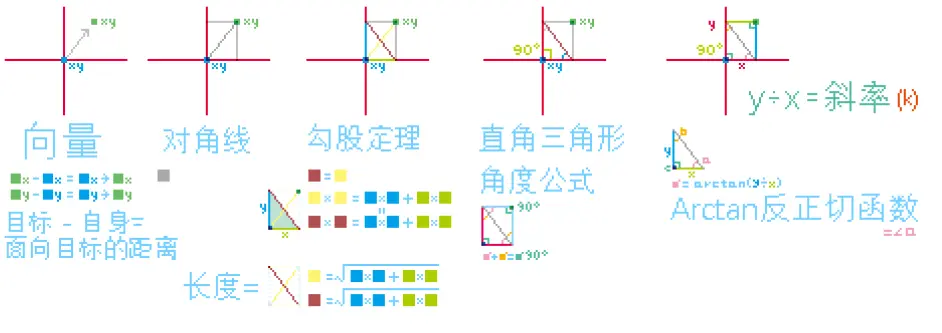
Godot学习笔记 向量转角度 面向坐标 Rad2deg和atan2 已知两点坐标求角度 哔哩哔哩
平行 角度 求め方
[最も欲しかった] ひし形面積公式 948629-ひし形面積公式
え形の面積の求め方を考えたり，面積の公式をつ 考え方の共通点を見つけて公式をつくり， 方くり出したりする。 その意味を説明することができる。 ・ 平行四辺形，台形，ひし形も同様に考え て，公式の意味を説明することができる。そこで、ひし形の面積の公式： ・ひし形の面積＝対角線×対角線÷2 ページの先頭へ 正方形の面積をひし形で考えてみよう 先ほど、「ひし形は正方形のお母さん筋に当たる図形」だと書きましたが、これは、正方形もひし形として面積を求めることが5年 面積1 子どもの学習支援 by いっちに算数 スマホ版 ① 三角形と平行四辺形と台形・ひし形の面積の求め方 ② 三角形と平行四辺形と台形・ひし形の面積求め方の公式 ③ いろいろな三角形・四角形の面積
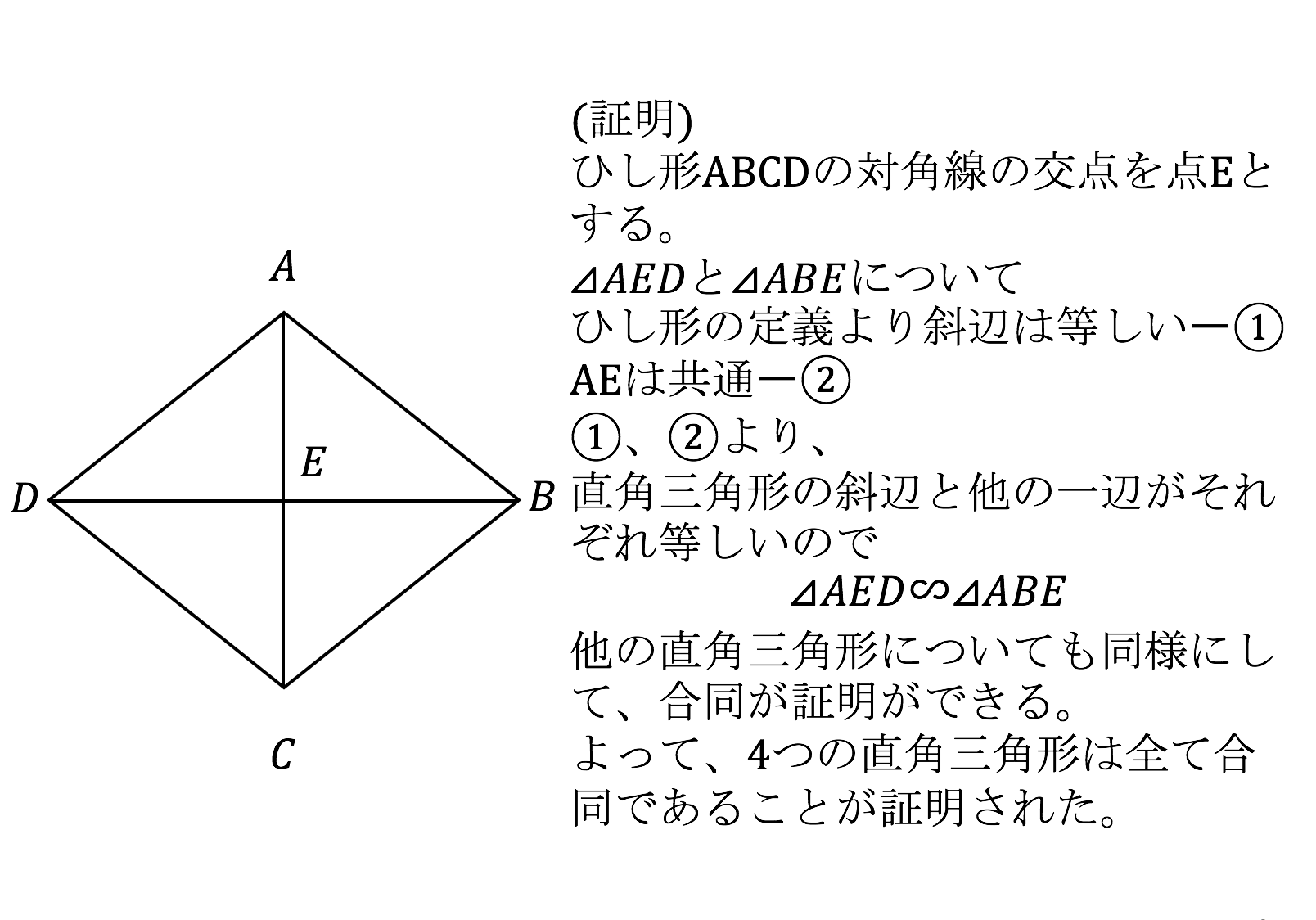
3分で分かる ひし形の面積の公式と問題の解き方をわかりやすく 合格サプリ
ひし形面積公式
コンプリート！ 三角形と四角形の角 420516-三角形と四角形の角
第2学年「三角形と四角形」 2 単元のねらい ・ 身の回りにあるものの形の中から、三角 形や四角形、長方形や正方形を見付けよう とする。 算数への関心・意欲・態度 ・ 辺や頂点などの構成要素に着目して、三 角形や四角形、長方形や正方形の特徴を見FdData 高校入試：中学数学2 年：三角形と四角形 仮定と結論，逆，合同条件／三角形の合同の証明／二等辺三角形の定理／ 二等辺三角形の性質を使った証明 ／二等辺三角形になることを証明／正三角形／ 直角三角形／三角形 四角形 年 組 くみ 名前 まえ 四角形 4本のまっすぐな線（直線）でかこまれた形を四角形といいます。 4つのかどがすべて直角な四角形を 4つのかどがすべて直角で、4つ 長方形といいます。 の辺の長さもすべて同じ四角形を 正方形といいます。
多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
三角形と四角形の角
[最も共有された！ √] 面積の求め方 小学生 333334-正三角形 面積の求め方 小学生
平面図形の面積・まわりの長さの求め方（公式）を一覧にまとめました。 公式を忘れてしまったときにはこちらで確認しましょう。 （基本的な問題もあわせて練習できるようになっています。） 円の面積・まわりの長さの求め方 ひし形の面積・まわりの長さの求め方 台形の面積の求め方4年算数 大きい面積の求め方 子どもの学習支援 by いっちに算数 スマホ版 前のページに戻る 教え方4 平方メートル の単位を教え、平方メートル と平方センチメートル の単位の関係に気づかせます。 そのあとで、㎝とmの単位を混合した正方形や長方形の面積を求める問題を考えさせます。 三角形の面積と，底辺と高さの関係について考える。 9 台形の面積の求め方を考える。 10 本時 平行四辺形を用いた倍積変形の方法をもとに、台形の面積を求める公式をつくる。 11 ひし形の面積の求め方を考える。 ひし形の面積を求める公式をつくる。 12
三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
正三角形 面積の求め方 小学生
コンプリート！ 四角形 の 面積 の 公式 898006-四角形の面積の公式
4 四角形の面積 公式のまとめ 1 四角形の種類と性質 四角形には、台形、平行四辺形、長方形、ひし形、正方形など、いろいろな形のものがあります。 台形は、向かい合う1組の辺が平行という条件だけを満たすものですが、平行四辺形になると特に，相似な三角形の面積比は相似比の二乗に比例することも分かります。 →相似比と面積比，体積比の公式の証明 また，サインの性質： sin θ = sin (18 0 ∘ − θ) \sin \theta=\sin (180^{\circ}\theta) sin θ = sin (18 0 ∘ − θ) に注意すると，円に内接する四角形 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。
すきるまドリル 小学５年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント
四角形の面積の公式
200以上 相似の問題 420964-相似の問題
数学35章図形と相似「平行線と線分の比」＜準備問題＞ 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ，条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。 公立高校入試 過去問 英語 お問い合わせ 全都道府県 公立高校入試 過去問 数学 4平面図形 4相似の証明ほか 10/18 公立高校入試 過去問 数学 目次 数学4．平面図形 4．相似の証明 複合問題ほか 数学4．平面図形 4．相似の証明 複合問題ほか 02年度相似 練習問題 相似1 (基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4 (発展) 相似5 相似6 角の二等分線と辺の比 (発展) 相似と面積比 面積比 ① 2組の辺の比とその間の角がそれぞれ等しい。 ③ 2組の角がそれぞれ等しい。 x=16cm, y=12cm (1) ABC∽ AED 2組の角がそれぞれ等しい (2)①AE=8cm ②DE= 16 3 cm
相似を使う問題 難問に挑戦 第１１回算数オリンピック ファイナル問題 中学入試算数６８分野別解法
相似の問題
登録:
投稿 (Atom)
