数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。 公立高校入試 過去問 英語 お問い合わせ 全都道府県 公立高校入試 過去問 数学 4平面図形 4相似の証明ほか 10/18 公立高校入試 過去問 数学 目次 数学4.平面図形 4.相似の証明 複合問題ほか 数学4.平面図形 4.相似の証明 複合問題ほか 02年度相似 練習問題 相似1 (基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4 (発展) 相似5 相似6 角の二等分線と辺の比 (発展) 相似と面積比 面積比 ① 2組の辺の比とその間の角がそれぞれ等しい。 ③ 2組の角がそれぞれ等しい。 x=16cm, y=12cm (1) ABC∽ AED 2組の角がそれぞれ等しい (2)①AE=8cm ②DE= 16 3 cm
相似を使う問題 難問に挑戦 第11回算数オリンピック ファイナル問題 中学入試算数68分野別解法
相似の問題
相似の問題-面積比を使った問題(中級編) 次の図で、 であるとき次の問いに答えなさい。 (1) と の面積比を求めなさい。 (2) と台形 の面積比を求めなさい。 なので、このように別々に書いてあげると見やすくなりますね。 この2つの三角形は相似になって 応用問題を解くには、当然、基本が分かっていないとできません。 ということで、まずは相似(合同)や比の問題で最初にやることを確認しておきます。 ①与えられた長さ、角度、比は図に書き込む ②比を求めたい場合は、比を求めたい直線を、1辺とし



中3数学相似問題 この問題の面積比の求め方がよく分かりません 教えてください Yahoo 知恵袋
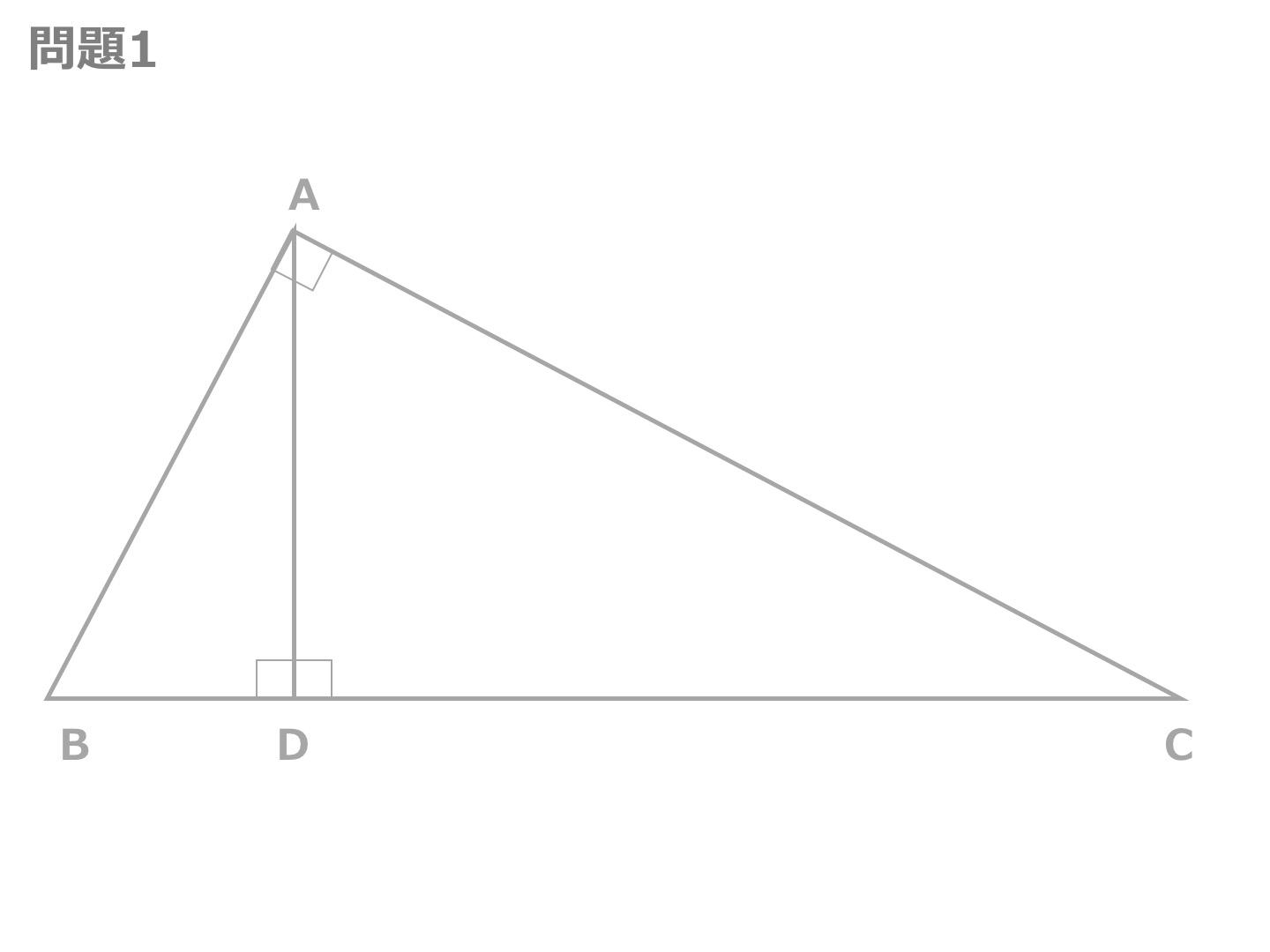
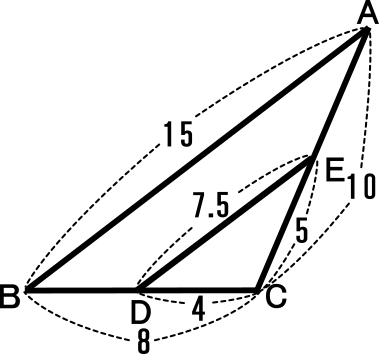
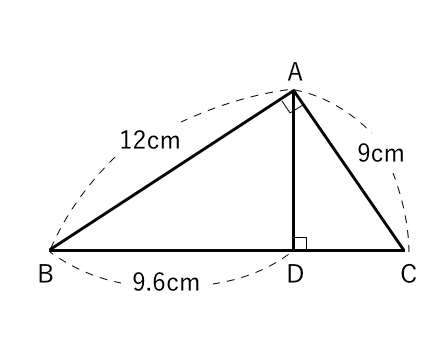
問題 ☆記述のポイント! 思考の深化 「ミックスピザはどっちがお得?」 ~相似比や面積比を利用し,日常生活の疑問を解決する~ ☆本時のねらい:相似な図形の相似比と面積比の関係を理解し,それを利用することが できる。面白い数学図形問題 (中3) カテゴリ: カテゴリ未分類 中2の K衛門 。 やはりカンどころがよくて、もうすっかり図形の苦手意識がなくなっている。 期末テスト数学は予定通り (? )余裕で100点。 で、先生から数学のライバルの子と2人だけに 特別出された学習1 直角三角形・図形の折り返しと相似 問題 右の図のような,∠ A = 90° の直角三角形 ABC があり, 頂点 A から辺 BC に垂線 AD をひく。
相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの「相似の位置」「相似の中心」は、問題的にはふくらましにくいので 定期テスト的、単発的な問題になると思われます → ページの先頭に戻る イ 三角形の相似条件を用いた図形の性質の論証 《 例 》 地面に垂直に立つ木の高さを求めましょう → ∠c = ∠f (太陽光の角度は同じ) ① ∠b = ∠e 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②をベースにしたものです。
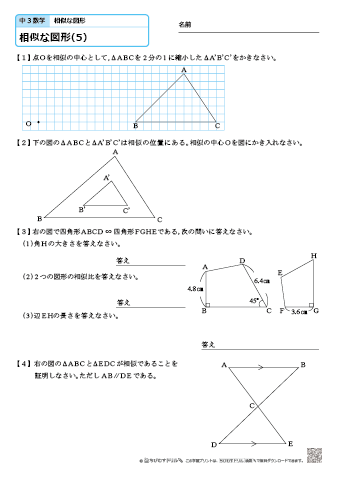
相似 練習問題 解答と解説 Hello School 算数 相似 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 1. 縮尺分の1の地図で60cmある道のりを時速60kmで行くと何分かかりますか。 解説: 縮尺分の1の地図で60cmは実際は 60×=cm=m=15km。 この道のりを時速60kmで進むと、中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!台形の面積比問題を解説! 円錐の体積比を解説!数学35章図形と相似「相似な図形」<基本問題①> 組 番 名前 A B C E (1)辺BCに対応する辺を答えなさい。 (2)四角形ABCDと四角形EFGHの相似比を求めなさい。 (3)辺EFの長さを求めなさい。 A D B C 60° 6cm 8㎝ E H F G 80° 6cm
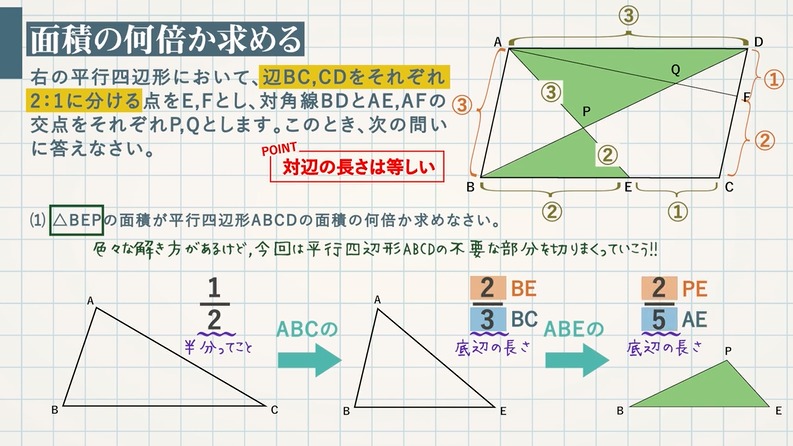



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



3
中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード・印刷 相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。SAPIX 6月マンスリー 算数問題(相似と比)台形と比(四谷大塚 合不合判定予備テストより)台形と面積比つづき(四谷大塚 合不合判定予備テストより)球の反射と相似(sapix サマーサポートより)長方形の折り返し(9月四谷大塚合不合判定テストより)三角形の相似と 苦手な人が多い図形の証明問題を解くコツを解説!実は非常に簡単なんです 年3月5日 証明なんて簡単!(整数編)に続いて、図形編です。 中学生の範囲においては、中学二年生の合同の証明と三年生で習う相似の証明です。 合同や相似には、合同条件・相似条件があります



相似が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
今後の目次 第4回 図形問題に強くなる②(相似の発見) ← 今週はココ! 第5回 図形問題に強くなる③(図形の移動) 第6回 規則性に強くなる 前回から図形問題を取り上げており、前回は円とおうぎ形を含む図形を題材に、補助線の効果的な引き方について説明いたし相似台形と面積比の問題を徹底解説! 相似な図形 中3相似中点連結定理、三等分の三角形求め方を問題解説! 相似な図形 中3数学相似な図形の見つけ方、相似条件とは?基本問題を使って解説! 相似な図形 これでバッチリ!相似の面積比を求める問題を相似な図形の面積比や体積比が! 4 4つの問題に挑戦しませんか 高校数学も,図形を使えば中学生にだって 5 数学の勉強法(?) 大層なものではありませんが・・・ 6 一筆(ひとふで)書きの秘密 あなたも一筆書きの天才(?)に! 7



Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 1 働きアリ The 2nd




Abcと Adeは正三角形で 相似の問題です 解き方教えてください Clear
中学3年生では初めての図形の単元です。 相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。 2年生の「 合同と証明 」などを軽くおさらいしてから取り組むと良いでしょう。 相似な図形(1) ⇒ 答え 円と相似に関する問題です。 円周角の定理を利用して、相似な三角形の証明をしたり、相似比を利用して長さを求めたりします。 基本的な問題は難しくないのでしっかり確認しておいてください。 よくある相似の証明 1 下の図で a相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。 台形については、補助線が
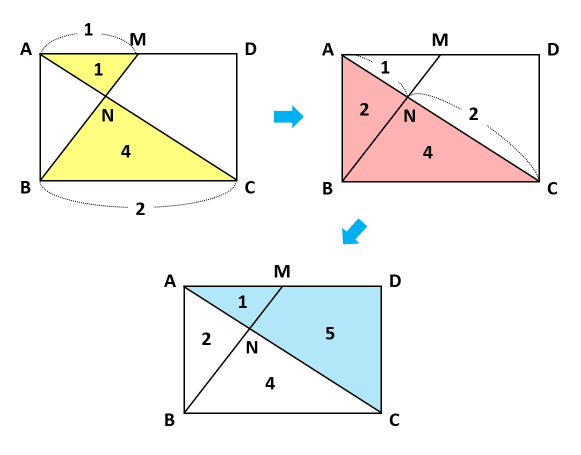



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



相似を使う問題 難問に挑戦 第11回算数オリンピック ファイナル問題 中学入試算数68分野別解法
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じまし相似比の練習問題(平行四辺形2) 問2. (1)mp:pc =1:2 (2) ncd の面積は3 cm 2 底辺が2倍の長さなので bpc は2 cm 2 ncd = bmc =1 +2 =3 問3. (1)bc:cp =3:1,ad =bc よりad:cp =3:1 =dq:qc なので dq =12 ×=9cm (2)底辺は3 倍,高さは4 倍なので12 倍2 問題の通りに図形が描けているか確認 3 平行や直角を見つける 31 隠れた平行 32 隠れた直角 4 証明問題を解くコツ4つ 41 1とにかく図形の性質や条件を覚える 42 2「仮定」と「結論」をチェック、仮定を図に書き込む 43 3結論を見て、覚えた図形の



図形問題が驚くほど得意になる基本問題とは あおぞら塾
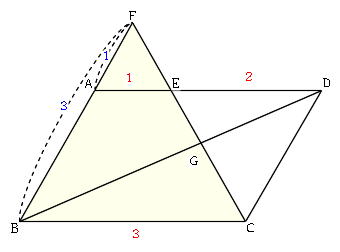



Mathematics 相似 3 平行線と比 みんなが苦手な相似頻出問題 働きアリ
③ イカ 相似 ④ ミミ 相似 平面図形 ポイント⑪ – 8つの典型図形 中学入試の算数における平面図形と比の問題では、平面図形のポイント⑩三角形の相似4パターン+以下の典型図形8パターン= 典型図形12パターン が繰り返し出てくる! 平面図形と比の相似な立体の表面積・体積(2) 6 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括高校入試(高校受験)数学・対策問題 » 中学数学相似と方程式 ;




いろいろな相似の証明 無料で使える中学学習プリント



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327
「相似」ならば(4)(5)(6)は言えるが,(4)(5)(6)から「相似」というためには「間の角が等しい」ことを追加しなければならない. 例題1 異なる4点 A, B, C, D が同一円周上にあって,線分 AB と線分 CD の交点を P とするとき常に相似である図形 問題(2 学期期末) 次の各組の図形は常に相似であるといえるか。いえる場合は ,いえない場合は×で答え よ。 (1) 2 つの二等辺三角形 (2) 2 つの正三角形 (3) 2 つの直角三角形 (4) 2 つのひし形 (5) 2 つの正五角形 解答欄 (1)第7問平行四辺形と相似 1日目 年 入試解説 兵庫 平行四辺形 灘 男子校 相似 相似比 ★★★☆☆☆(中学入試標準レベル)
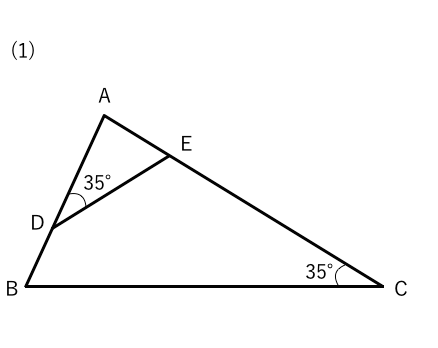



相似な図形 相似条件の練習問題 苦手な数学を簡単に
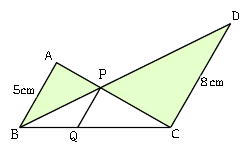



Mathematics 相似 3 平行線と比 みんなが苦手な相似頻出問題 働きアリ
「相似な図形」のパターンがある? 実は、三角形の相似の問題では、 よく使われる 「基本の形」 が2つあります。 その2つとは 「ちょうちょ型」 と 「ピラミッド型」 です。 これらが見えれば、 "相似形だ!"と分かるのです。 見つけ方のコツ ですね。 いろいろな相似の証明 相似な図形の証明問題です。 入試でもよく出題されるので、いろいろな問題を解くようにして見てください。 ポイント 図の中で証明する三角形に印をつけて、相似条件に当てはまるかを考えてみてください。 すぐに解けない場合は、解答 16年11月10日 / Last updated 18年12月5日 parako 数学 中3数学 相似な図形問題 下の図の三角形 \(abc\) において、点 \(d\) は辺 \(ab\) 上の点であり、 \(ab=ac\) 、\(ad=cd=cb=1cm\) である。辺 \(ab\) の長さを求めなさい。 解説 まずこの二等辺三角形の配置が有名配置であることを 知っておきたいです。 二
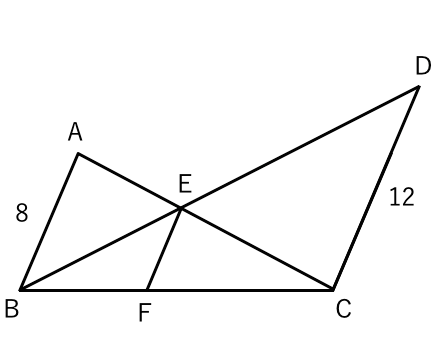



相似の問題 テスト 受験対策 苦手な数学を簡単に




世界一わかりやすい数学問題集中3 5章 図形と相似
相似 練習問題 相似1(基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4(発展) 相似5 相似6 角の二等分線と辺の比(発展) 相似と面積比 面積比相似 練習問題 相似1(基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4(発展) 相似5 相似6 角の二等分線と辺の比(発展) 相似と面積比 面積比
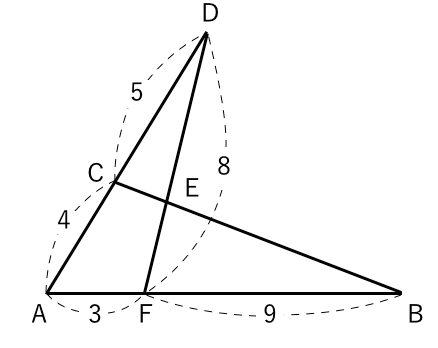



相似の問題19 テスト 受験対策 苦手な数学を簡単に




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
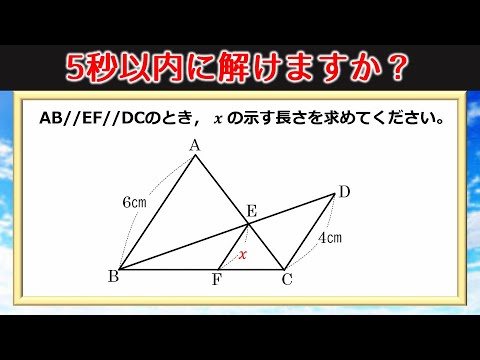



図形問題 知っている人は5秒で解ける相似の裏技 Youtube



すぐるゼミ 相似な図形の応用
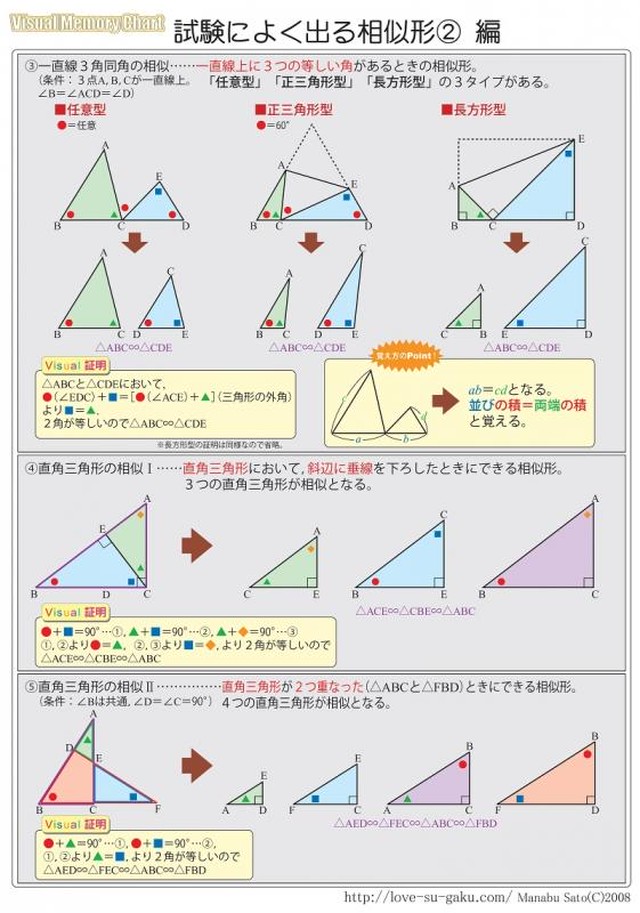



数学 試験によく出る相似形が完璧にわかるまとめ集 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru
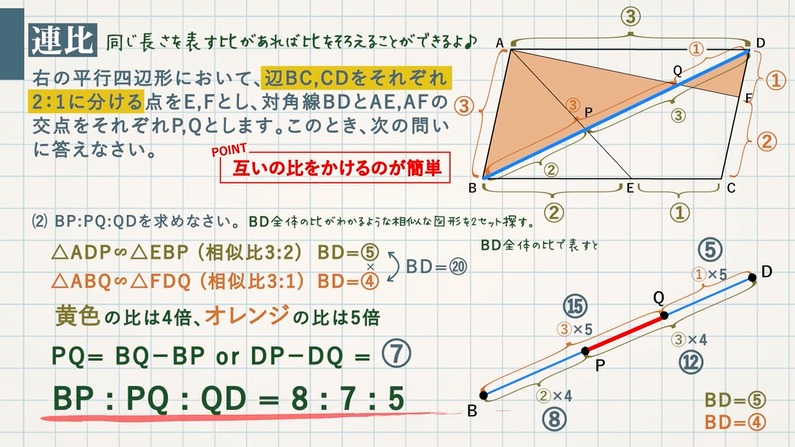



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者




図形の相似 の問題のわからないを5分で解決 映像授業のtry It トライイット
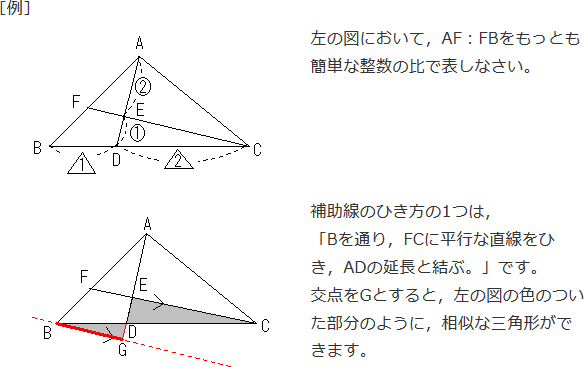



相似な図形 補助線を引いて考える相似の問題 中学数学 定期テスト対策サイト




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
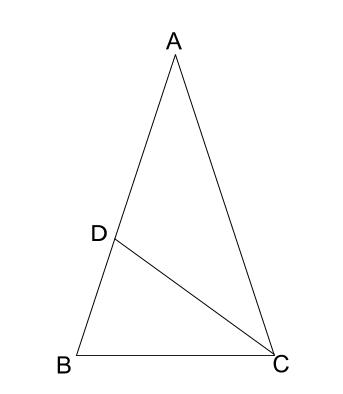



中学数学 相似と方程式 中学数学の無料オンライン学習サイトchu Su
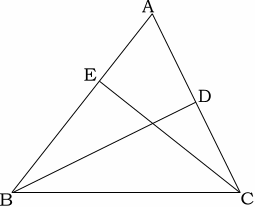



相似の証明2
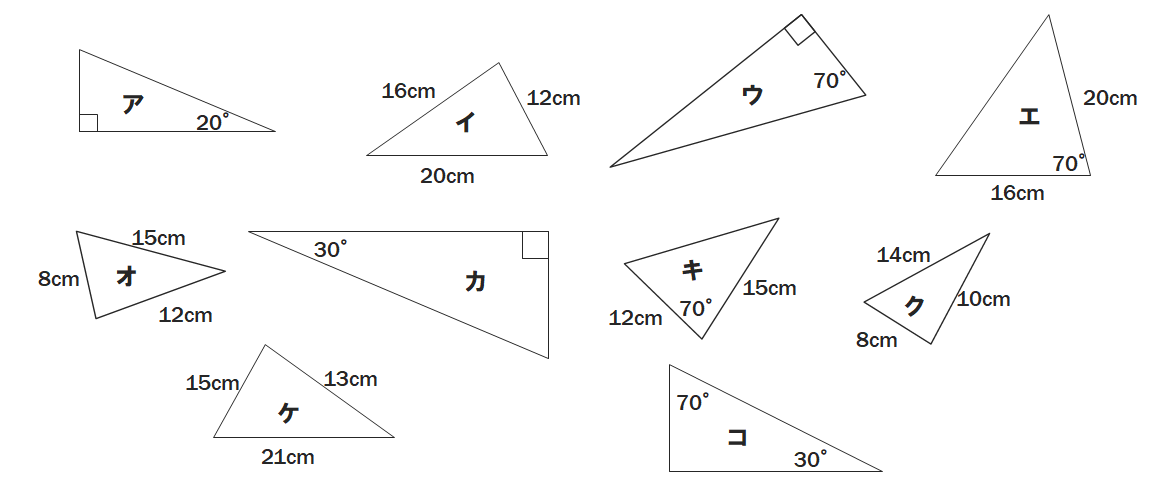



中3数学 相似な図形の線分比の定期テスト対策問題 Examee




図形と相似 Qikeru 学びを楽しくわかりやすく



相似図形




合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam




難関中学に合格する 相似形と面積比 図形の移動トレーニング 入試によく出る図形問題106問 増補改訂4版 通販 セブンネットショッピング




中学数学の図形相似問題を解説してください Okwave



1
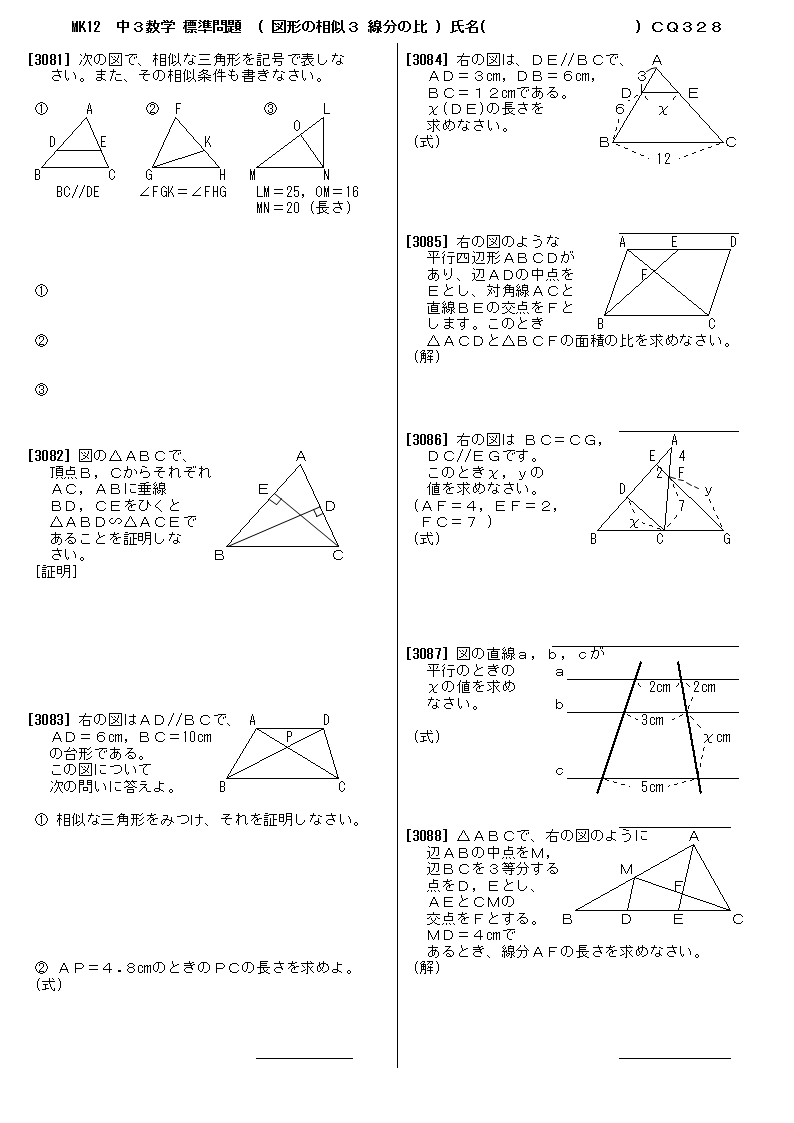



無料 中3数学 標準問題 問題プリント 328 図形の相似3 線分の比




中3 相似証明問題 この下のような証明問題の場合どことどこの図形でやるか Okwave




数学 相似の問題 三角形の面積 相似の問題なのですが わからない問題が Okwave




相似 算数星人のweb問題集 中学受験算数の問題に挑戦



中3数学 相似の 差がつく 問題 成績 上がってます 根城学習塾 八戸市
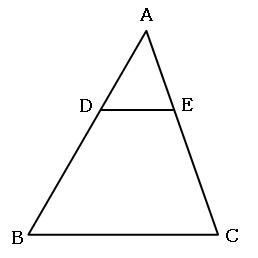



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし
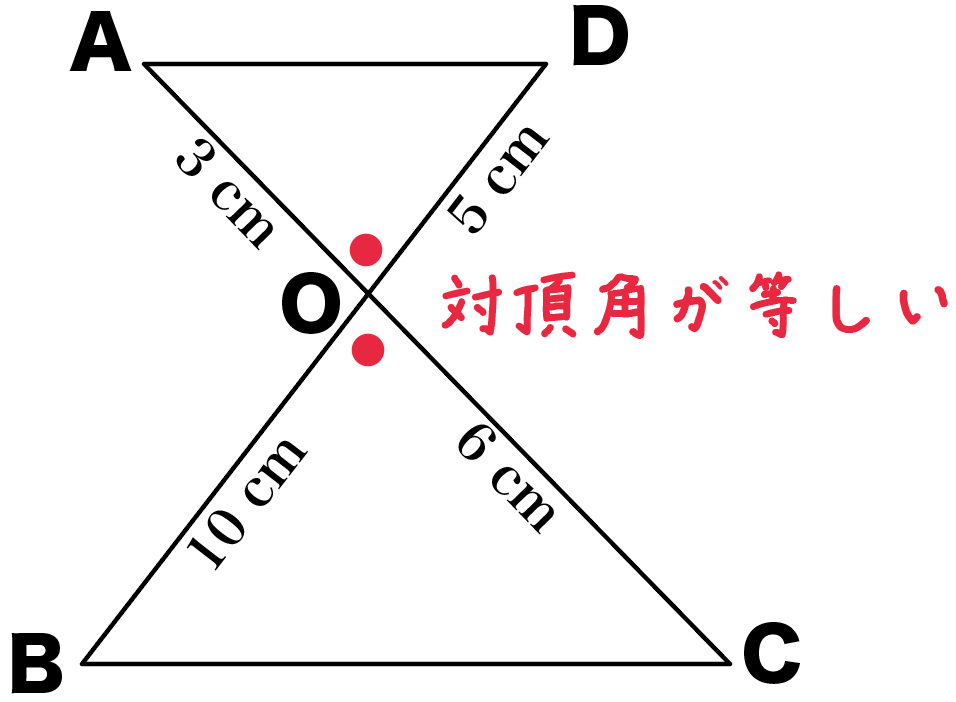



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



中学数学単元別 相似な図形 数学 中学校 教材 問題集 305 学林舎 通販 Yahoo ショッピング



高校入試数学 相似な三角形の対策問題



Q Tbn And9gcte8fsqvrlckxdilyd5wnblxavnplfa7mg7ddvhyyrzhuvjel Usqp Cau



U9j580gf8iba369ji2w Xyz P 1096




相似 平行四辺形と面積比の問題を徹底解説 数スタ



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328



高校入試 英語 数学 図形と相似 重要問題
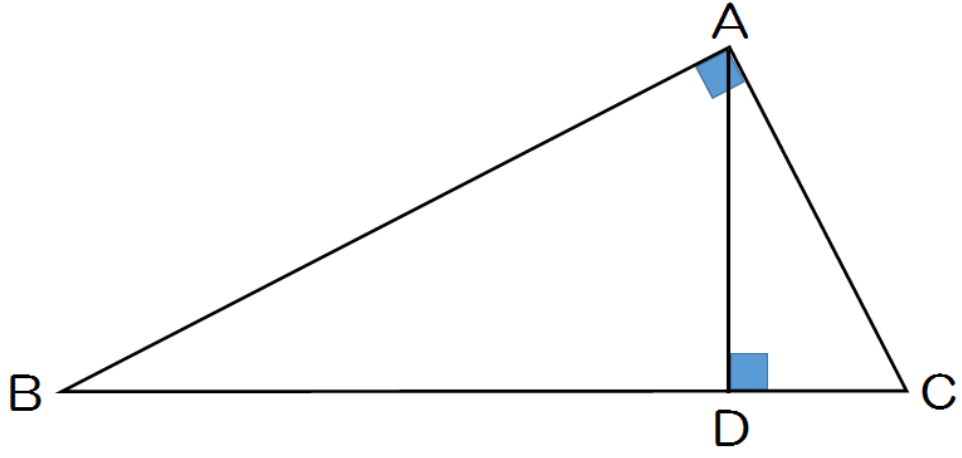



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく
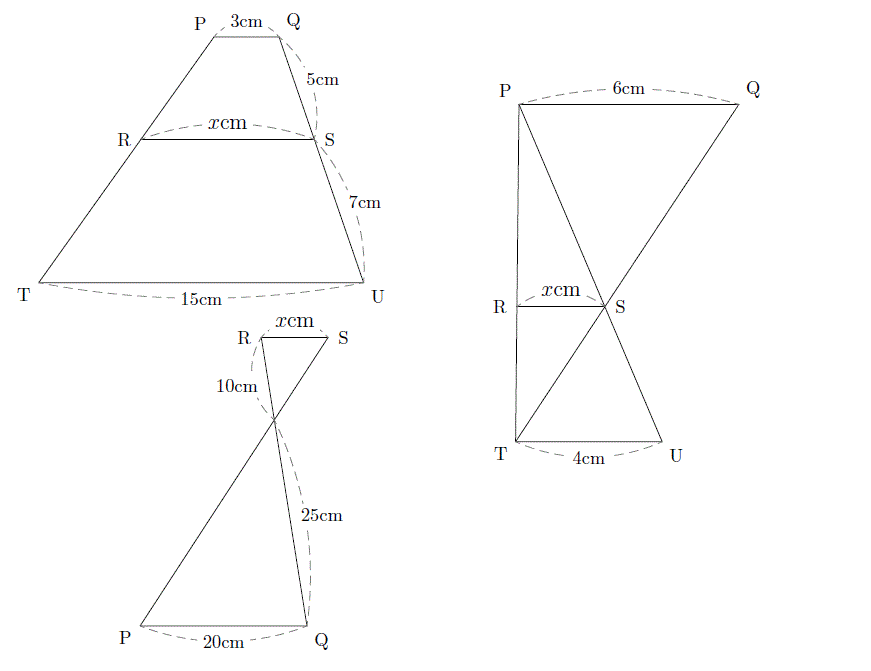



かみのドリル 相似



相似の応用 1 問題の考え方と解き方




相似を利用した色々な問題 チーム エン



中学3年数学練習問題 三角形の相似条件と証明の問題




中学3年の数学 動画 相似と面積 基本編の問題 19ch




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




意外と解けない相似問題 中3教科書レベルの基本問題 暇つぶしに動画で脳トレ



相似の応用 時習館 ゼミナール 高等部



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法




職業訓練試験用対策 忘れた方勉強方法が分からない方のための相似の問題解説例題集 ふくなんログ



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ The 2nd



1




難関中学に合格する 相似形と面積比 図形の移動トレーニング 改訂3版 Yell Books 井上慶一 本 通販 Amazon



開成中学入試問題 算数 を徹底解説 平成29年度 算数 大問3 1 相似の図形ー第2回 星一徹式ゲリラ中学受験



相似の問題 テスト 受験対策 苦手な数学を簡単に



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



図形と証明 相似 スタディーx
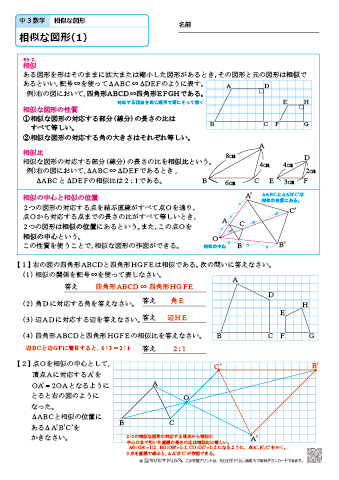



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 5章 図形と相似



中3数学相似問題 この問題の面積比の求め方がよく分かりません 教えてください Yahoo 知恵袋



面積比問題より 相似比の間違い これが中学入試に出た図形問題




中3数学 相似比とは 例題編 映像授業のtry It トライイット




三平方の定理と相似の問題 無料で使える中学学習プリント




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似




難関中学に合格する 相似形と面積比 図形の移動トレーニング 改訂4版 絵本ナビ 井上 慶一 みんなの声 通販




相似じゃない三角形の面積比の求め方がよく分かりません Clear




相似比の利用 スタディーx




数学 中3 53 相似と面積 応用編 Youtube




三角形の相似条件と証明問題の解き方 数学fun
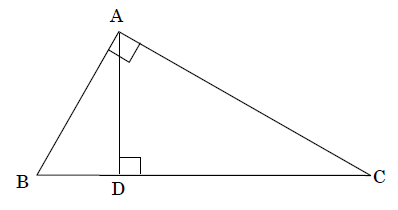



中3数学 いろいろな相似の証明の特訓練習問題 Atstudier



相似図形をさがす問題



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
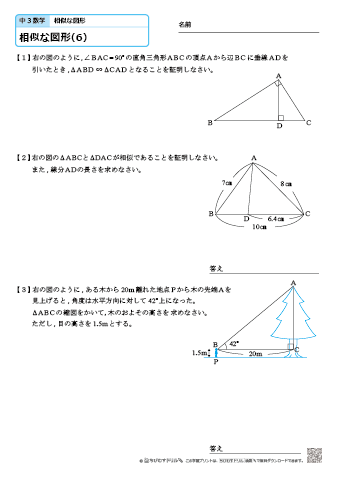



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校入試対策数学 面積比に関する対策問題 Pikuu




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 2 働きアリ




相似の問題10 テスト 受験対策 苦手な数学を簡単に
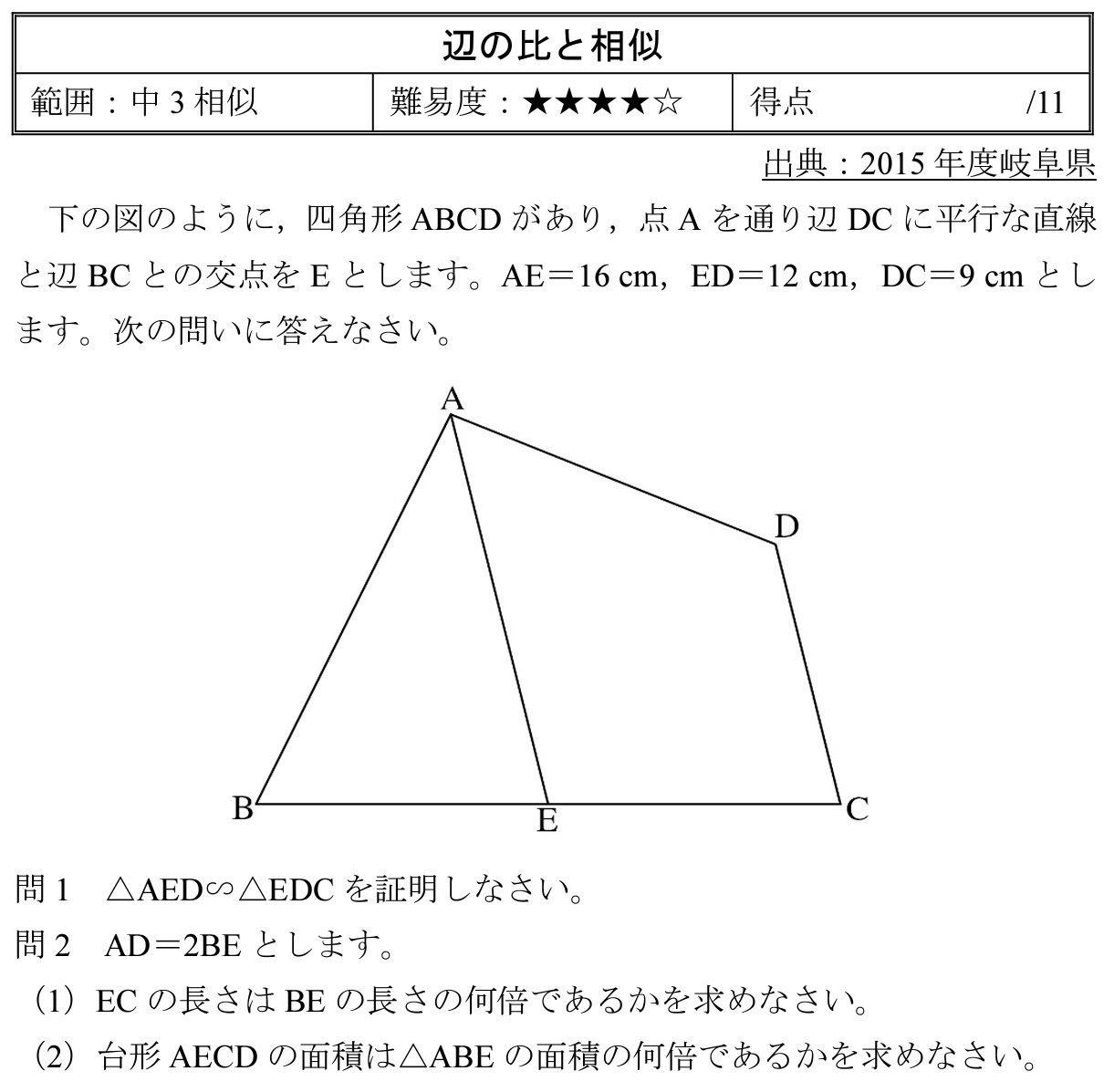



相似比辺の比 15年度岐阜県 高校入試 数学 良問 難問




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題
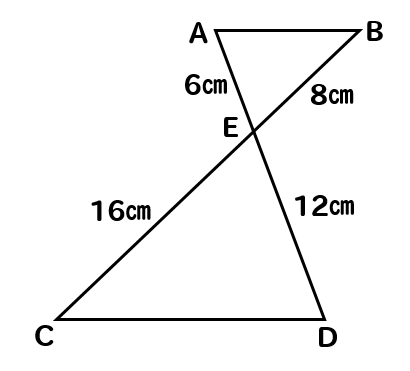



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




世界一わかりやすい数学問題集中3 5章 図形と相似
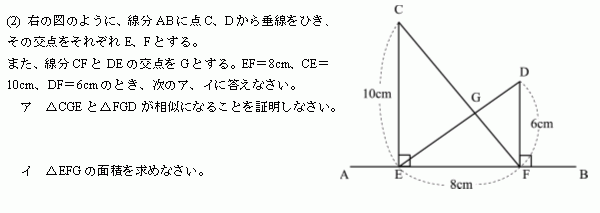



相似比の利用 無料学習プリント教材




都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




裏返しの相似 数学のすすめ
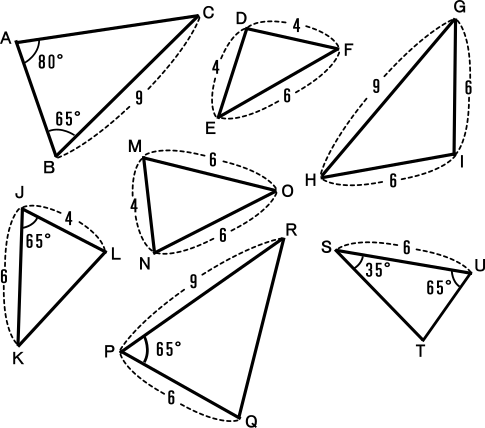



中学3年数学練習問題 三角形の相似条件の問題
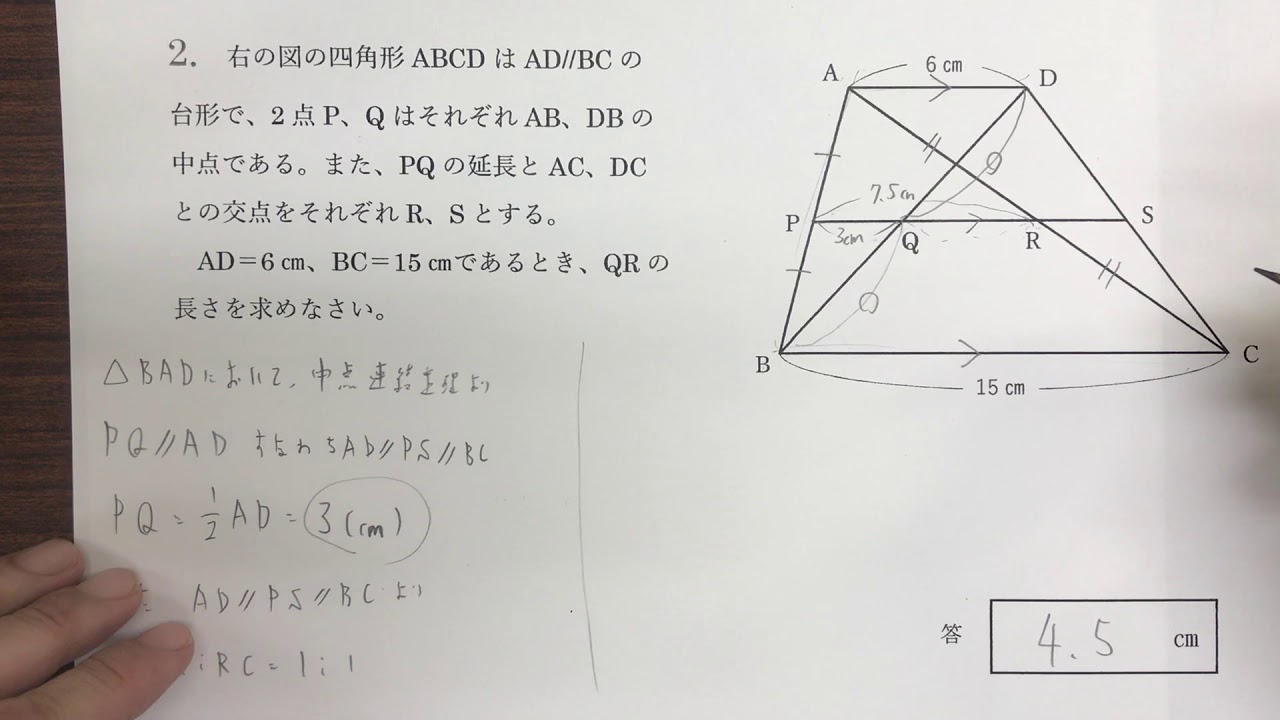



図形 証明 応用問題 相似中心 大問2 中学数学単元別強化教材 これから 図形 紹介動画 3年生2学期レベル Youtube




世界一わかりやすい数学問題集中3 5章 図形と相似




三角形の面積比と相似比 チーム エン
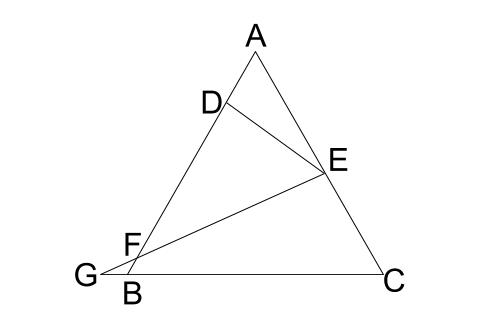



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su



0 件のコメント:
コメントを投稿