
三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori
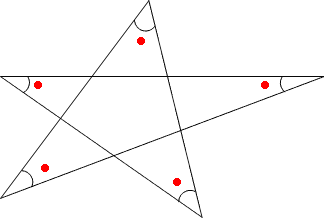
角度の求め方 算数の教え上手 学びの場 Com
平行四辺形のなかの三角形の相似や角度、長さ、等しい面積の求め方 中学の数学の解き方の詳しい解説ノートです。ノートの取り方も参考にしてください。ノートはクリックで拡大します。 現役 三角形の面積は「 底辺 高さ 底 辺 × 高 さ ÷ 2 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形
答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を 三角関数の角度を求めるときは、θの範囲を忘れないこと それぞれの求め方をまとめると 単位円 を書いて、三角関数に適した直線を書き込み交点を求める。 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるか二等辺三角形の2つの底角は等しいです。 よって、 ∠ C の大きさも 50 ∘ です。 よって、 ∠ B ∠ C = 100 ∘ です。 三角形の内角の和は 180 ∘ なので、 ∠ A の大きさは、

角度の求め方 算数の教え上手 学びの場 Com
三角形証明(発展1) 3 3 次の図で abcは∠abc=90°の直角二等辺三角形である。aとcから直線mにおろした垂線の交点をそれぞれd,eとする。 「中学校数学学習サイト」には基礎問題から入試にも対応した発展問題まで幅広いレベルの問題が多数掲載されてい合同の証明 証明とは 仮定や図形の性質を根拠として結論を導く。 等式を用いて説明するが、どの式にも 理由が必要 である。 三角形の合同を証明する 三角形の合同条件をそろえることで証明できる 例1 cはadの中点で, ∠bac=∠edcのとき bac≡ edcとなること 相似の証明の簡単な問題が載っけてあります! 答えは丁寧に書かれているのでいらないところは、省略してください (答えは後半にあります) 学年 中学3年生, 教科書 未来へひろがる数学3 啓林館, 単元 図形と相似, キーワード 数学,相似の証明,相似,math
中3第1章23式の計算の利用 整数の性質の証明 中学数学 1学期
平行是一個幾何學術語。 在平面幾何中,永遠不會相交的多條直線,或者多個平面彼此互相平行。 在歐幾里得幾何中,由平行公設,一個平面上的直線外指定一個點,就能指定出一條與它平行的直線。 在非歐幾何中,根據空間曲率的不同,在一條直線外指定一個點可以作多條或零條與它平行的直線。753 两平面的夹角 定义 两张平面的法向量的夹角(通常指 锐角 )称为 两平面的夹角 。 设平面Π 1 和Π 2 为: 它们的法向量依次为: 、 , 记平面Π 1 和Π 2 的夹角 ,由规定 应是锐角,因此 的余弦值非负。 (6) 从两向量垂直、平行的充分必要条件立即推得下列结论:平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 1
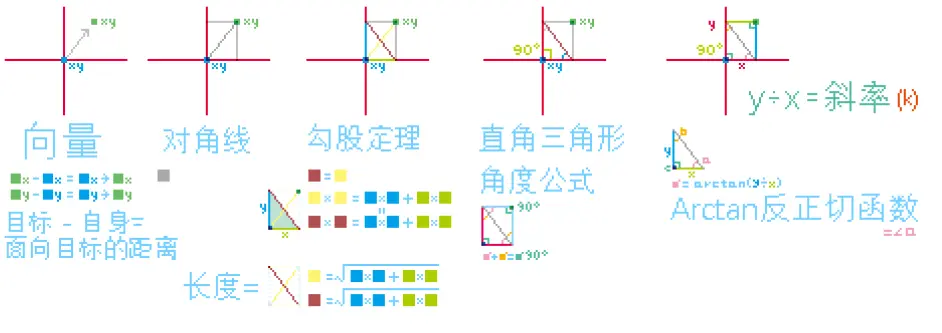
Godot学习笔记 向量转角度 面向坐标 Rad2deg和atan2 已知两点坐标求角度 哔哩哔哩
